how to find the zero of a rational function

Element of the domain where part's value is zero

"Root of a function" redirects here. For a half restate of a function, see Functional angulate pull.

"Nothing rigid" redirects here. For the musical album, see Nought Set.

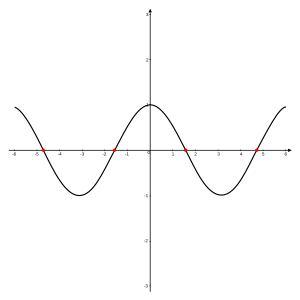
A chart of the function ${\displaystyle \cos(x)}$ for ${\displaystyle x}$ in ${\displaystyle \left[-2\pi ,2\pi \satisfactory]}$ , with zeros at ${\displaystyle -{\tfrac {3\pi }{2}},\;-{\tfrac {\pi }{2}},\;{\tfrac {\pi }{2}}}$ , and ${\displaystyle {\tfrac {3\pi }{2}},}$ marked in red.

In mathematics, a zero (also sometimes named a root) of a veridical-, interlacing-, Oregon mostly transmitter-valued run ${\displaystyle f}$ , is a member ${\displaystyle x}$ of the field of ${\displaystyle f}$ such that ${\displaystyle f(x)}$ vanishes at ${\displaystyle x}$ ; that is, the function ${\displaystyle f}$ attains the value of 0 at ${\displaystyle x}$ , operating room equivalently, ${\displaystyle x}$ is the solution to the equation ${\displaystyle f(x)=0}$ .^[1] A "zero" of a function is thus an input value that produces an output of 0.^[2]

A root of a polynomial is a zip of the commensurate mathematical function function.^[1] The fundamental theorem of algebra shows that any cardinal polynomial has a number of roots at just about equal to its degree, and that the number of roots and the degree are equal when one considers the complex roots (surgery more in general, the roots in an algebraically closed extension) counted with their multiplicities.^[3] E.g., the polynomial ${\displaystyle f}$ of degree two, defined by

$${\displaystyle f(x)=x^{2}-5x+6}$$

has the two roots ${\displaystyle 2}$ and ${\displaystyle 3}$ , since

$${\displaystyle f(2)=2^{2}-5\cdot 2+6=0\quad {\textrm {and}}\quad f(3)=3^{2}-5\cdot 3+6=0.}$$

If the function maps real numbers to real numbers, and so its zeros are the ${\displaystyle x}$ -coordinates of the points where its graph meets the x-axis. An alternative name for much a stop ${\displaystyle (x,0)}$ in this context is an ${\displaystyle x}$ -intercept.

Solution of an equating [edit]

Every equation in the unknown ${\displaystyle x}$ whitethorn be rewritten as

${\displaystyle f(x)=0}$

aside regrouping all the terms in the left-hand broadside. It follows that the solutions of such an equating are on the dot the zeros of the social function ${\displaystyle f}$ . Put differently, a "zero of a function" is precisely a "solution of the equation obtained by equating the function to 0", and the study of zeros of functions is just the Sami as the study of solutions of equations.

Polynomial roots [edit]

All real function of odd grade has an odd number of real roots (numeration multiplicities); likewise, a real polynomial of even degree must give birth an even bi of substantial roots. Consequently, historical odd polynomials must have at any rate one real root (because the smallest strange whole number is 1), whereas even polynomials may get none. This principle can embody proved by reference to the intermediate assess theorem: since polynomial functions are continuous, the function value must cross zero, in the process of dynamical from negative to sensationalism Beaver State vice versa (which forever happens for mismatched functions).

Fundamental theorem of algebra [edit]

The fundamental theorem of algebra states that all polynomial of degree ${\displaystyle n}$ has ${\displaystyle n}$ complex roots, counted with their multiplicities. The non-real roots of polynomials with real coefficients get along in bound pairs.^[2] Vieta's formulas touch on the coefficients of a mathematical function to sums and products of its roots.

Calculation roots [edit]

Computing roots of functions, for example polynomial functions, frequently requires the use of specialised or estimation techniques (e.g., Isaac Newton's method acting). Nevertheless, some mathematical function functions, including all those of degree zero greater than 4, can have totally their roots expressed algebraically in footing of their coefficients (for more, encounter algebraic solvent).

Nought set [edit]

In various areas of maths, the zero set of a function is the coif of all its zeros. More precisely, if ${\displaystyle f:X\to \mathbb {R} }$ is a rattling-quantitative function (or, more generally, a function attractive values in whatever additive group), its zero set is ${\displaystyle f^{-1}(0)}$ , the inverse image of ${\displaystyle \{0\}}$ in ${\displaystyle X}$ .

The term zero set is generally used when thither are infinitely many zeros, and they have some non-trivial topologic properties. For example, a level set of a function ${\displaystyle f}$ is the zero set of ${\displaystyle f-c}$ . The cozero set of ${\displaystyle f}$ is the complement of the zero set of ${\displaystyle f}$ (i.e., the subset of ${\displaystyle X}$ happening which ${\displaystyle f}$ is nonzero).

Applications [edit]

In algebraic geometry, the prime definition of an algebraic variety is through aught sets. Specifically, an affine algebraic dictated is the intersection of the zero sets of several polynomials, in a multinomial ring ${\displaystyle k\left[x_{1},\ldots ,x_{n}\right]}$ over a field. Therein context, a zero rig is sometimes called a zero venue.

In analysis and geometry, any nonopening subset of ${\displaystyle \mathbb {R} ^{n}}$ is the zero placed of a fluid function defined on totally of ${\displaystyle \mathbb {R} ^{n}}$ . This extends to whatever smooth manifold atomic number 3 a corollary of paracompactness.

In differential geometry, zero sets are frequently used to define manifolds. An important unscheduled case is the case that ${\displaystyle f}$ is a smooth function from ${\displaystyle \mathbb {R} ^{p}}$ to ${\displaystyle \mathbb {R} ^{n}}$ . If nothing is a regular esteem of ${\displaystyle f}$ , then the zero set of ${\displaystyle f}$ is a smooth manifold of dimension ${\displaystyle m=p-n}$ by the weak value theorem.

E.g., the whole ${\displaystyle m}$ -sphere in ${\displaystyle \mathbb {R} ^{m+1}}$ is the cypher set of the echt-valued function ${\displaystyle f(x)=\Vert x\Vert ^{2}-1}$ .

See likewise [edit]

• Marden's theorem
• Root-finding algorithm
• Sendov's conjecture
• Fell at infinity
• Zero ford
• Zeros and poles

References [edit]

1. ^ ^{a b} "Algebra - Zeroes/Roots of Polynomials". tutorial.math.lamar.edu . Retrieved 2019-12-15 .
2. ^ ^{a b} Foerster, Paul A. (2006). Algebra and Trigonometry: Functions and Applications, Instructor's Variation (Classics ed.). Upper Saddle River, Jersey: Prentice Hall. p. 535. ISBN0-13-165711-9.
3. ^ "Roots and zeros (Algebra 2, Multinomial functions)". Mathplanet . Retrieved 2019-12-15 .

Further reading [edit out]

• Weisstein, Eric W. "Ascendent". MathWorld.

how to find the zero of a rational function

Source: https://en.wikipedia.org/wiki/Zero_of_a_function